先の投稿では画像検索に関する基本的な動作確認を行いましたが、その中で以下のような感触を得ました。
- 同じ被写体を撮影したものであれば、ある程度位置をずらして撮影したものでも類似度が高いと判断される
- 同じ被写体を撮影したものでも、構図(被写体の向きや撮影時のアングル)が違うと類似度が低く判断されがち
- 違う被写体を撮影したものでも、色合いや構図が似ていると類似度が高いと判断されてしまう
- 同一の被写体と判断して良さそうな距離の境界は、コサイン距離の場合、0.2前後になりそう
今回はもう少し際どい(判断が難しいと思われる)画像での類似度判定を確認してみたいと思います。
実験データ
被写体としては卓上カレンダーを使用します。
期待するのは1月の面と2月の面を見分けることです。
各面に関しては3タイプの撮影方法で、それぞれ3枚の画像を作成しました。
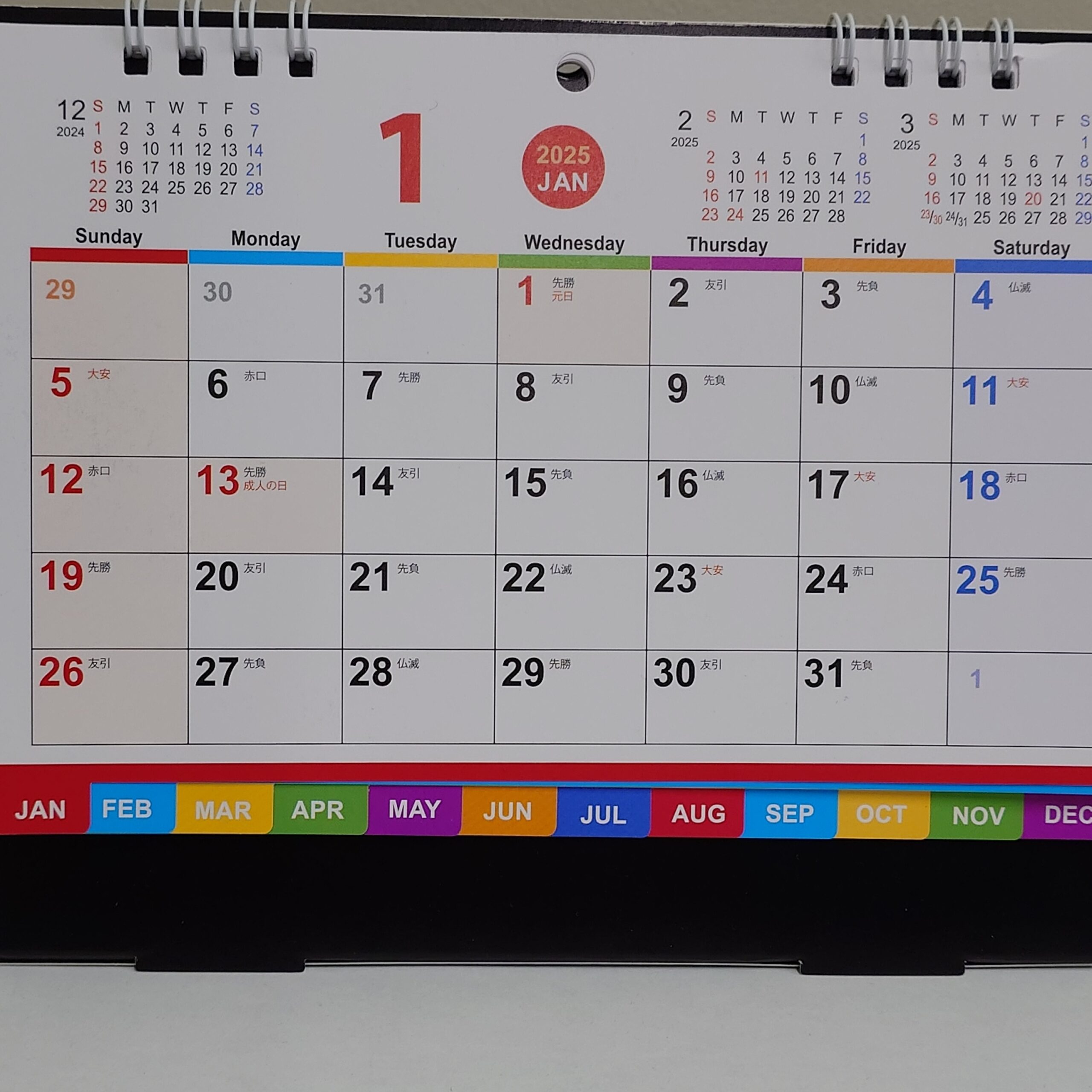
1月 / グループ1(1-1)
 |  |  |
| 1.jpg | 2.jpg | 3.jpg |
1月の面を撮影したもので、カレンダーの横幅が画像一杯になるように心掛けて撮影したものです。
1月 / グループ2(1-2)
 |  |  |
| 4.jpg | 5.jpg | 6.jpg |
1月の面に対して、グループ1よりも少し引いて、カレンダーの横に隙間ができるような距離で撮影したものです。
1月 / グループ3(1-3)
 |  |  |
| 7.jpg | 8.jpg | 9.jpg |
1月の面に対して、グループ1よりも接写気味に撮影したもので、カレンダー以外の写り込みがより少なくなっています。
2月 / グループ1(2-1)
 |  |  |
| 10.jpg | 11.jpg | 12.jpg |
2月の面に対して「1月 / グループ1」と同等の撮影をしたものです。
2月 / グループ2(2-2)
 |  |  |
| 13.jpg | 14.jpg | 15.jpg |
2月の面に対して「1月 / グループ2」と同等の撮影をしたものです。
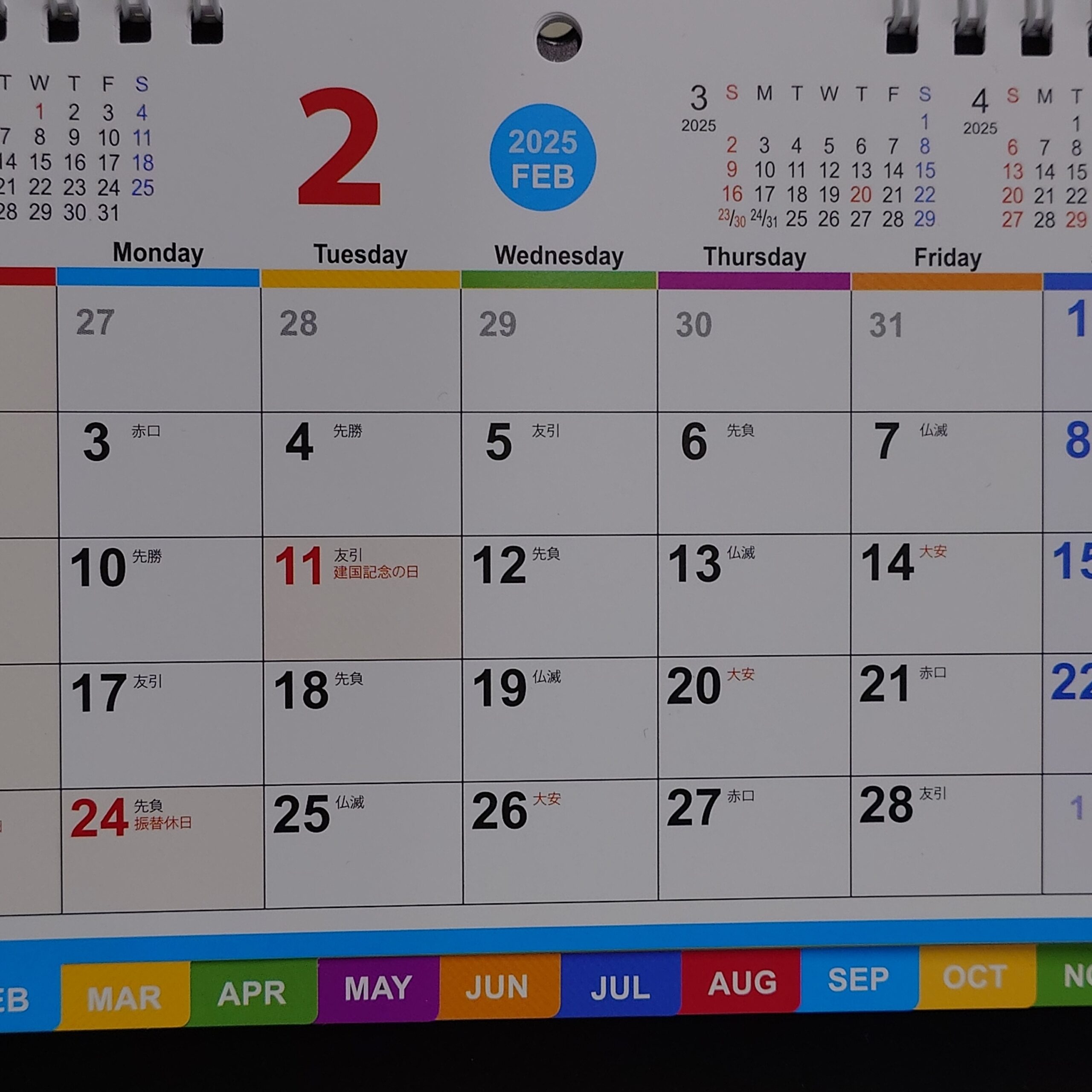
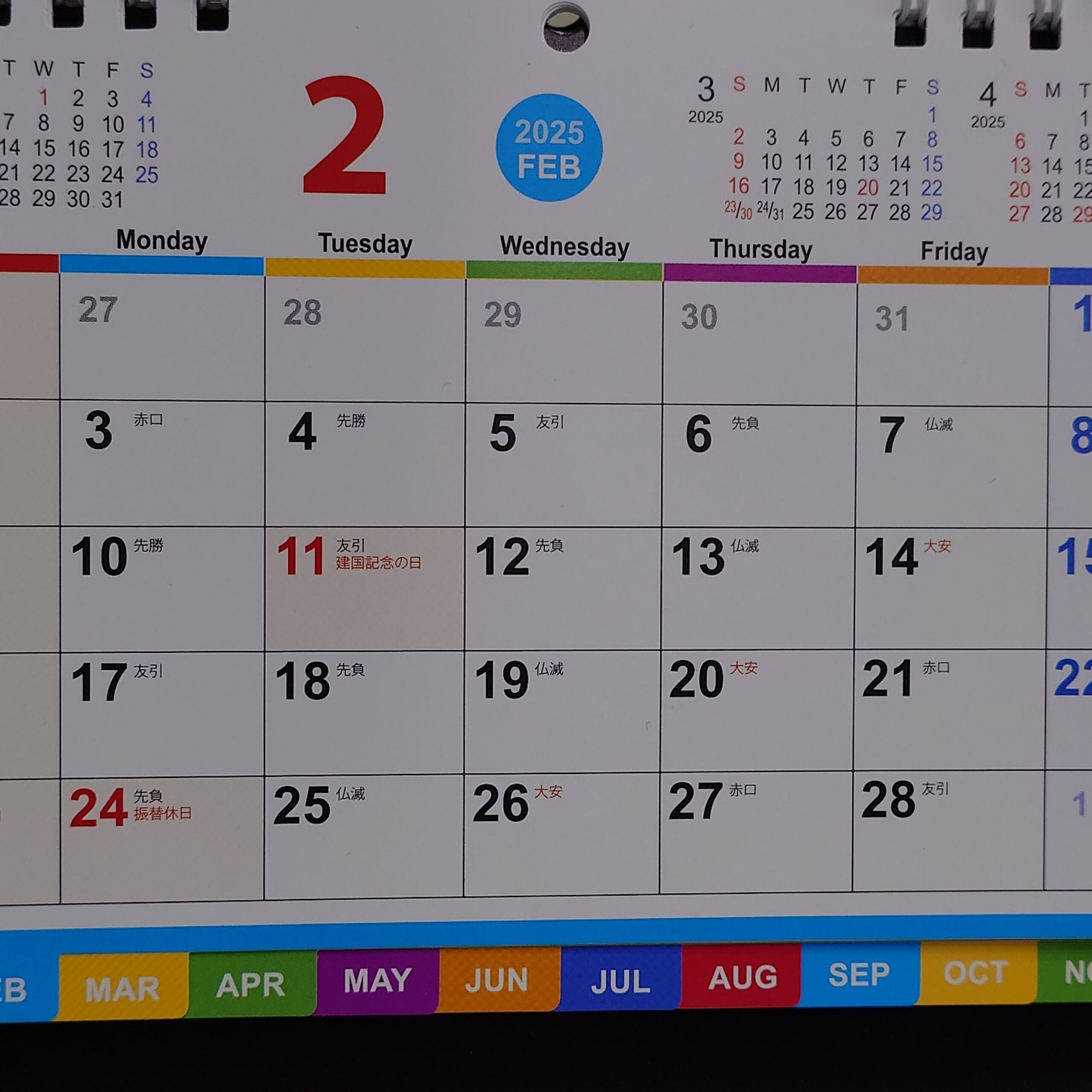
2月 / グループ3(2-3)
 |  |  |
| 16.jpg | 17.jpg | 18.jpg |
2月の面に対して「1月 / グループ3」と同等の撮影をしたものです。
実験結果
1月の面を写した各画像に対して、他の画像との距離を計測した結果を以下に列記します。
エンベディングの処理は前回と同じものを使用し、距離としてもコサイン距離を採用しています。
なお、比較対象が同一グループに属するケースを赤字、別グループでも同じ月の面を写したものであればオレンジで記述してあります。
1.jpg
| 1.JPG | 0.0 | 1-1 |
| 2.JPG | 0.02784925304069108 | 1-1 |
| 3.JPG | 0.02995325864034326 | 1-1 |
| 12.JPG | 0.03552994165855905 | 2-1 |
| 10.JPG | 0.036375036946671546 | 2-1 |
| 11.JPG | 0.040210460322456565 | 2-1 |
| 4.JPG | 0.07031636901888982 | 1-2 |
| 5.JPG | 0.08222984429967595 | 1-2 |
| 6.JPG | 0.08907303947046252 | 1-2 |
| 15.JPG | 0.09452619156324449 | 2-2 |
| 14.JPG | 0.09513289022318216 | 2-2 |
| 17.JPG | 0.09945597077768287 | 2-3 |
| 18.JPG | 0.09965222781414607 | 2-3 |
| 13.JPG | 0.10044197294671176 | 2-2 |
| 16.JPG | 0.1289576579824464 | 2-3 |
| 9.JPG | 0.15330151584149654 | 1-3 |
| 7.JPG | 0.21490731325282342 | 1-3 |
| 8.JPG | 0.2797069449149202 | 1-3 |
同一グループの画像は他の画像よりも距離が近いと判断されました。
一方で、同じ1月の面を写した他のグループ(1-2,1-3)よりも、2月の面を写したものでありながら構図の類似性が高いグループ2-1の方が距離が近いと判断されてしまっています。
グループ1-1に対して1-2や2-2の方が1-3や2-3よりも距離が近いと判断されていますが、これは1-1の構図と比較した場合の被写体とカメラ間の距離の変化が1-3,2-3の方が大きくなっていて、結果として絵的な変化の度合いも大きくなっているためと考えられます。
2.jpg
| 2.JPG | 0.0 | 1-1 |
| 1.JPG | 0.02784925304069108 | 1-1 |
| 3.JPG | 0.03107656234195255 | 1-1 |
| 10.JPG | 0.03208861894620685 | 2-1 |
| 11.JPG | 0.03322064679588377 | 2-1 |
| 12.JPG | 0.03892119517764203 | 2-1 |
| 4.JPG | 0.06163640348727362 | 1-2 |
| 6.JPG | 0.06526447722333006 | 1-2 |
| 15.JPG | 0.07257610980493168 | 2-2 |
| 13.JPG | 0.07588466412787664 | 2-2 |
| 14.JPG | 0.07676650001919916 | 2-2 |
| 17.JPG | 0.08461575098110086 | 2-3 |
| 5.JPG | 0.0853098760251394 | 1-2 |
| 18.JPG | 0.09602927208163636 | 2-3 |
| 16.JPG | 0.11766997645814115 | 2-3 |
| 9.JPG | 0.1367732909616377 | 1-3 |
| 7.JPG | 0.20085736630523066 | 1-3 |
| 8.JPG | 0.2662858256178501 | 1-3 |
傾向的には「1.jpg」のケースと同等です。
3.jpg
| 3.JPG | 0.0 | 1-1 |
| 1.JPG | 0.02995325864034326 | 1-1 |
| 2.JPG | 0.03107656234195255 | 1-1 |
| 10.JPG | 0.04432798139414407 | 2-1 |
| 12.JPG | 0.04836783070418771 | 2-1 |
| 11.JPG | 0.05064519226462694 | 2-1 |
| 6.JPG | 0.06815783530930442 | 1-2 |
| 4.JPG | 0.08396799610096983 | 1-2 |
| 18.JPG | 0.0852899380623614 | 2-3 |
| 17.JPG | 0.08633698893184039 | 2-3 |
| 5.JPG | 0.08905747634926264 | 1-2 |
| 14.JPG | 0.10517852258922677 | 2-2 |
| 13.JPG | 0.10609201413879865 | 2-2 |
| 16.JPG | 0.10821151697123488 | 2-3 |
| 9.JPG | 0.11523690152629162 | 1-3 |
| 15.JPG | 0.11999416801099494 | 2-2 |
| 7.JPG | 0.1536719350848087 | 1-3 |
| 8.JPG | 0.21891666494020545 | 1-3 |
傾向的には「1.jpg」のケースと同等です。
4.jpg
| 4.JPG | 0.0 | 1-2 |
| 5.JPG | 0.033924140843635264 | 1-2 |
| 6.JPG | 0.050694441506121235 | 1-2 |
| 11.JPG | 0.05991494737964609 | 2-1 |
| 2.JPG | 0.06163640348727362 | 1-1 |
| 14.JPG | 0.062181952116275085 | 2-2 |
| 10.JPG | 0.06397917796747132 | 2-1 |
| 13.JPG | 0.06420016132437123 | 2-2 |
| 12.JPG | 0.06464303687888984 | 2-1 |
| 1.JPG | 0.07031636901888982 | 1-1 |
| 15.JPG | 0.07229393854196287 | 2-2 |
| 3.JPG | 0.08396799610096983 | 1-1 |
| 18.JPG | 0.15084931290992665 | 2-3 |
| 17.JPG | 0.15160554760153033 | 2-3 |
| 16.JPG | 0.16987020631502403 | 2-3 |
| 9.JPG | 0.18415913260740424 | 1-3 |
| 7.JPG | 0.23244320171373123 | 1-3 |
| 8.JPG | 0.2801590329566951 | 1-3 |
傾向的には「1.jpg」のケースと同等です。
構図の類似度(1-2に対する2-2)の優位性がグループ1-1のケースほど顕著ではありませんが、大きな違いとは言えないかと。
5.jpg
| 5.JPG | 0.0 | 1-2 |
| 4.JPG | 0.033924140843635264 | 1-2 |
| 6.JPG | 0.04531411186463408 | 1-2 |
| 12.JPG | 0.06924746902171064 | 2-1 |
| 14.JPG | 0.07258272184199488 | 2-2 |
| 10.JPG | 0.07295565458377629 | 2-1 |
| 11.JPG | 0.07860481054423707 | 2-1 |
| 13.JPG | 0.08167646039381493 | 2-2 |
| 1.JPG | 0.08222984429967595 | 1-1 |
| 2.JPG | 0.0853098760251394 | 1-1 |
| 3.JPG | 0.08905747634926264 | 1-1 |
| 15.JPG | 0.09140781887303351 | 2-2 |
| 18.JPG | 0.1540747967246877 | 2-3 |
| 17.JPG | 0.16042195923653269 | 2-3 |
| 9.JPG | 0.1780687759108759 | 1-3 |
| 16.JPG | 0.18142138108277184 | 2-3 |
| 7.JPG | 0.20651611182317842 | 1-3 |
| 8.JPG | 0.24123172555592143 | 1-3 |
傾向的には「4.jpg」のケースと同等です。
6.jpg
| 6.JPG | 0.0 | 1-2 |
| 5.JPG | 0.04531411186463408 | 1-2 |
| 4.JPG | 0.050694441506121235 | 1-2 |
| 2.JPG | 0.06526447722333006 | 1-1 |
| 11.JPG | 0.06544830089344367 | 2-1 |
| 10.JPG | 0.06601523808550536 | 2-1 |
| 14.JPG | 0.0661409573237387 | 2-2 |
| 12.JPG | 0.06759458256422068 | 2-1 |
| 3.JPG | 0.06815783530930442 | 1-1 |
| 13.JPG | 0.06959101670946666 | 2-2 |
| 1.JPG | 0.08907303947046252 | 1-1 |
| 15.JPG | 0.09995954346617864 | 2-2 |
| 18.JPG | 0.1351040635383649 | 2-3 |
| 17.JPG | 0.1371582627219493 | 2-3 |
| 9.JPG | 0.14880821586335224 | 1-3 |
| 16.JPG | 0.15110871627013922 | 2-3 |
| 7.JPG | 0.18174330571901476 | 1-3 |
| 8.JPG | 0.22079448939854818 | 1-3 |
傾向的には「4.jpg」のケースと同等です。
7.jpg
| 7.JPG | 0.0 | 1-3 |
| 8.JPG | 0.03466749667334956 | 1-3 |
| 9.JPG | 0.058354447412779065 | 1-3 |
| 3.JPG | 0.1536719350848087 | 1-1 |
| 18.JPG | 0.17233766343255008 | 2-3 |
| 16.JPG | 0.17331320378584758 | 2-3 |
| 17.JPG | 0.1790979882211261 | 2-3 |
| 6.JPG | 0.18174330571901476 | 1-2 |
| 2.JPG | 0.20085736630523066 | 1-1 |
| 5.JPG | 0.20651611182317842 | 1-2 |
| 1.JPG | 0.21490731325282342 | 1-1 |
| 10.JPG | 0.22967359844653157 | 2-1 |
| 12.JPG | 0.23219891327359932 | 2-1 |
| 4.JPG | 0.23244320171373123 | 1-2 |
| 11.JPG | 0.2504768447012974 | 2-1 |
| 13.JPG | 0.2925612776877524 | 2-2 |
| 14.JPG | 0.2935112443690967 | 2-2 |
| 15.JPG | 0.32603505125588395 | 2-2 |
同一グループの画像が他の画像よりも距離が近いと判断されている点は今までのケースと同様ですが、同一グループ以外の画像との比較における距離がより大きくなっています。
これは、接写することでカレンダーに印字されている内容がより大写しになっており、画像の差として認識され易くなったためと推測します。
8.jpg
| 8.JPG | 0.0 | 1-3 |
| 7.JPG | 0.03466749667334956 | 1-3 |
| 9.JPG | 0.09926764667420196 | 1-3 |
| 3.JPG | 0.21891666494020545 | 1-1 |
| 6.JPG | 0.22079448939854818 | 1-2 |
| 5.JPG | 0.24123172555592143 | 1-2 |
| 18.JPG | 0.24856410167029008 | 2-3 |
| 16.JPG | 0.25507135592008645 | 2-3 |
| 17.JPG | 0.25996634143142394 | 2-3 |
| 2.JPG | 0.2662858256178501 | 1-1 |
| 1.JPG | 0.2797069449149202 | 1-1 |
| 4.JPG | 0.2801590329566951 | 1-2 |
| 12.JPG | 0.2803880429091242 | 2-1 |
| 10.JPG | 0.28631918680311697 | 2-1 |
| 11.JPG | 0.3108177349888851 | 2-1 |
| 13.JPG | 0.3561627567231612 | 2-2 |
| 14.JPG | 0.36110324437209707 | 2-2 |
| 15.JPG | 0.3906195949497807 | 2-2 |
傾向的には「7.jpg」のケースと同等です。
9.jpg
| 9.JPG | 0.0 | 1-3 |
| 7.JPG | 0.058354447412779065 | 1-3 |
| 16.JPG | 0.08886326695397395 | 2-3 |
| 18.JPG | 0.09393377087045629 | 2-3 |
| 17.JPG | 0.09669651664196266 | 2-3 |
| 8.JPG | 0.09926764667420196 | 1-3 |
| 3.JPG | 0.11523690152629162 | 1-1 |
| 2.JPG | 0.1367732909616377 | 1-1 |
| 6.JPG | 0.14880821586335224 | 1-2 |
| 1.JPG | 0.15330151584149654 | 1-1 |
| 10.JPG | 0.16704488697763786 | 2-1 |
| 12.JPG | 0.16991397114315354 | 2-1 |
| 5.JPG | 0.1780687759108759 | 1-2 |
| 11.JPG | 0.18256048488601084 | 2-1 |
| 4.JPG | 0.18415913260740424 | 1-2 |
| 13.JPG | 0.22429458005395908 | 2-2 |
| 14.JPG | 0.2243330020794292 | 2-2 |
| 15.JPG | 0.2453458115470124 | 2-2 |
傾向的には「4.jpg」のケースと同等ですが、同一グループに属する「8.jpg」が、グループ2-3の各画像よりも距離が遠いと判断されています。
「8.jpg」と「9.jpg」を良く見比べてみると、「8.jpg」は若干明るく、「9.jpg」は若干暗く写っていて、一方でグループ2-3の画像は「9.jpg」の画像よりもさらに暗めに写っています。
この明暗の度合いによって、グループ2-3の方が「8.jpg」よりも類似度が高いと判断されたのではないかと推測します。
考察
改めて各比較結果から以下の観点で距離を抽出します。
- 最も近いと判断された画像との距離
- 同一グループで最も遠いと判断された画像との距離
- 異なる面(2月)を写したもので最も近いと判断された画像との距離
- 同じ面(1月)を写したもので最も遠いと判断された画像との距離
結果は以下の通り。
| 1.JPG | 2.JPG 0.02784925304069108 | 3.JPG 0.02995325864034326 | 12.JPG 0.03552994165855905 | 8.JPG 0.2797069449149202 |
| 2.JPG | 1.JPG 0.02784925304069108 | 3.JPG 0.03107656234195255 | 10.JPG 0.03208861894620685 | 8.JPG 0.2662858256178501 |
| 3.JPG | 1.JPG 0.02995325864034326 | 2.JPG 0.03107656234195255 | 10.JPG 0.04432798139414407 | 8.JPG 0.21891666494020545 |
| 4.JPG | 5.JPG 0.033924140843635264 | 6.JPG 0.050694441506121235 | 11.JPG 0.05991494737964609 | 8.JPG 0.2801590329566951 |
| 5.JPG | 4.JPG 0.033924140843635264 | 6.JPG 0.04531411186463408 | 12.JPG 0.06924746902171064 | 8.JPG 0.24123172555592143 |
| 6.JPG | 5.JPG 0.04531411186463408 | 4.JPG 0.050694441506121235 | 11.JPG 0.06544830089344367 | 8.JPG 0.22079448939854818 |
| 7.JPG | 8.JPG 0.03466749667334956 | 9.JPG 0.058354447412779065 | 18.JPG 0.17233766343255008 | 4.JPG 0.23244320171373123 |
| 8.JPG | 7.JPG 0.03466749667334956 | 9.JPG 0.09926764667420196 | 18.JPG 0.24856410167029008 | 4.JPG 0.2801590329566951 |
| 9.JPG | 7.JPG 0.058354447412779065 | 8.JPG 0.09926764667420196 | 16.JPG 0.08886326695397395 | 4.JPG 0.18415913260740424 |
上記から以下のようなことが言えるかと思います。
- 最も近いと判断された場合でも0.02以上の距離がある
- 異なる被写体でも見た目の類似性が高いもの(カレンダーの1月と2月)であれば、被写体自体の差よりも構図等の差の方が距離への影響度が大きい
- 同一の被写体で、構図等も合わせたつもりでも、若干の撮影状況の違いにより0.1程度の距離と判断されてしまう場合がある
- 同一被写体でも、少し構図が変わることで0.2以上の距離と判断されてしまう場合がある
- 異なる被写体でも構図や撮影状況の類似度が高ければ0.1未満の距離と判断されてしまう
- 見た目の類似度が高い被写体でも、その差が十分視認できる程度の解像度であれば距離に反映され易いと思われる
まとめ
結果を大雑把にまとめれば、「現在の方式では今回対象としたレベルの類似性を持つ被写体を識別するには不十分な精度」と言うことになります。
類似度が高いと言っても、人間の目では簡単に識別できるレベルなのですが。
エンベディングに際して被写体の特徴がどの程度ベクトルに反映されるかが重要ですが、グループ1-3との比較の際にも触れたように、画像上のその特徴が十分確認できる状況になければ、その可能性は当然ながら低くなります。
改めて考えてみると、エンベディングの際に画像サイズを224×224に変換しており、今回使用した画像の細かさでは同変換時に小さな文字が潰れてしまい、特徴として反映され難くなってしまっているのかもしれません。
エンベディングに際して対象画像のサイズを大きくできるらしいとの未確認情報もあるのですが、それができたとしても処理速度の劣化に繋がる可能性は高くなりそうで、実際に判別精度が向上するかどうかも含めて実験が必要になります。
先の投稿でも触れたように、深層学習モデルや距離の算出方法を変えることで判別精度が向上することも期待できなくはないので、今後色々な可能性を探っていきたいと思います。
