前回の投稿では、エンベディングの前処理として背景除去、被写体サイズの均一化、画像サイズ(アスペクト比)統一を行うことでの識別精度向上を目指しました。
結果としては、「ある程度効果があるものの十分ではない」という結論に至りましたが、その際に以下の課題を残しました。
- 撮影時の明るさ、光の質、方向などにより、被写体の見え方(色合い等)に差異が生じることへの対策
- ボトルに写り込んだ周辺の状況が被写体自体の模様のように誤認される可能性への対策
2の観点での対処は難しそうなので、まずは1の観点でGemini先生に施策の提案をお願いしたところ、「ヒストグラム平坦化」なる方策をご教示いただきましたので、今回はこれを試してみたいと思います。
ヒストグラム平坦化
早速、Gemini先生に「ヒストグラム平坦化」に関して解説していただきましょう。
まずは「ヒストグラム」から。
画像内の各輝度値(通常は0〜255の範囲で表現される)の出現頻度をグラフにしたものです。横軸が輝度値、縦軸がその輝度値を持つピクセル数を示します。要は画像の輝度の分布状況をグラフ化したものと言ったところでしょうか。
上記を踏まえて、「ヒストグラム平坦化」について聞いてみましょう。
多くの画像では、輝度値が特定の範囲に偏っていることがあります。例えば、明るい画像では高輝度値にピクセルが集中し、暗い画像では低輝度値にピクセルが集中します。このような偏りがあると、画像のコントラストが低くなり、全体的にぼやけた印象になります。
ヒストグラム平坦化は、この輝度値の偏りを解消し、ヒストグラムをできるだけ均等に分布させることを目指します。これにより、画像のコントラストが向上し、明暗のメリハリがはっきりとした見やすい画像になります。つまり、輝度が均等に分布した状態になるように画像加工すること、と言う解釈で良いかと。
輝度値の偏りを解消することに加えて、明暗のメリハリがはっきりとした見やすい画像になるようです。
なお、ヒストグラム平坦化はグレースケール画像に対して適用される処理らしいです。
確かにネット情報でもグレースケール画像を対象としたものが大半でした。
色に関する情報を無視する形になる点は気になりますが、まずは実際に試してみることにしましょう。
画像処理
当然ながら、ヒストグラム平坦化の具体的な方法に関してもGemini先生に教えてもらいました。
trimmed_image = output_image[y:y+h, new_x:new_x+new_w]
resized_image = cv2.resize(trimmed_image, (224, 448))
# ヒストグラム平坦化
gray = cv2.cvtColor(resized_image, cv2.COLOR_RGBA2GRAY)
equalized_img = cv2.equalizeHist(gray)最初の2行は、前回の投稿で紹介した画像処理の最後の部分で、被写体を囲む適切な矩形への切り抜きを行い、その結果を224×448にリサイズしています。
その後に上記のようにヒストグラム平坦化の処理を追加しています。
ヒストグラム平坦化はグレースケール画像に対して適用されるものなので、まずはグレースケール化を行なっています。
その後にヒストグラム平坦化を行なっていますが、ここでも関数コール一発です。
「equalize(均等にする)Histogram(ヒストグラム)」ってことですね。
Pythonパネェっす。
対象画像(加工後)
使用する画像は前回の投稿と同じです(画像名表記も同様)。
結果は以下の通り。
比較しやすいようにヒストグラム平坦化を行なっていない画像(前回生成)と並べてあります。
被写体1
 |  |  |  |  | |
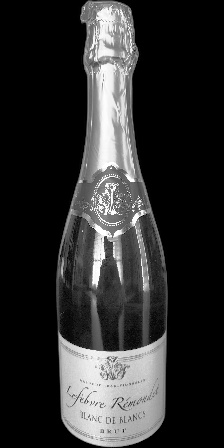 |  |  |  |  | |
| 1_Z | 1_L | 1_S | 1_G | 1_T | |
 |  |  |  |  |  |
 | 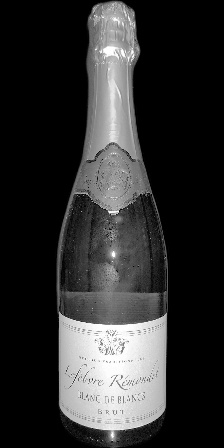 | 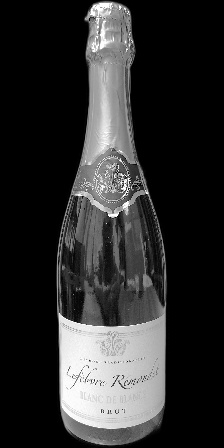 |  |  | 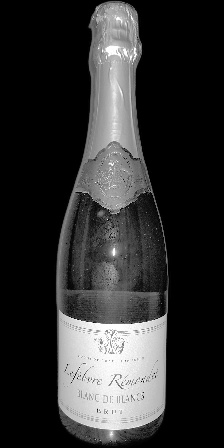 |
| 1_Z_N | 1_Z_N_F | 1_L_N | 1_L_N_F | 1_S_N | 1_S_N_F |
被写体2
 |  |  |  |  | |
 |  |  |  |  | |
| 2_Z | 2_L | 2_S | 2_G | 2_T | |
 |  |  |  |  |  |
 |  |  |  |  |  |
| 2_Z_N | 2_Z_N_F | 2_L_N | 2_L_N_F | 2_S_N | 2_S_N_F |
確かに前回の画像と比較して、被写体の視認性が大きく向上しています。
画像ごとの明暗の違いもほとんど感じられません。1_Z_Nと1_Z_N_Fを比較すると、前回の画像ではかなり印象が違うのですが、今回の画像では相当に近い印象を持ちます。
一方で、もう一つの懸念点であったボトルへの周辺状況の写り込みに関しては、より目立つようになってしまっています。
1_L_Nや2_L_Nでは、前回の画像では写り込みがほとんど視認できないレベルですが、今回の画像ではしっかり確認できます。
この辺がどの程度影響するのかは気になるところです。
なお、1_Z_Nや2_Z_N_Fを見ると前回の投稿で触れたボトル底面の認識が前回の画像と今回の画像で違っています。
これは前回から今回の間にPythonの実行環境に変化(パッケージの更新)があったことが関係していると推測されます。
試行錯誤の中である種のパッケージをインストールした際に関連パッケージとしてかなりの数のパッケージに更新が行われていたので、その影響ではないかと推測します(前回の結果と今回の結果を比較する上では環境が変わることは本来避けるべきなのですが)。
少なくとも、ヒストグラム平坦化とは無関係です。
距離測定
前回と同様に以下の観点で情報を抽出します。
- 対象画像と同じ被写体で最も近いもの
- 対象画像と同じ被写体で最も遠いもの
- 対象画像と異なる被写体で最も近いもの
- 対象画像と異なる被写体で最も遠いもの
また、期待する順序性と異なる結果が出た箇所に関しては赤字で示しています。
なお、今回は全体を俯瞰的に見られるように一覧化しました。
スペースの都合上、距離に関しては小数点以下6桁までで切り捨てにしてあります。
| 対象 | 同近 | 距離 | 同遠 | 距離 | 異近 | 距離 | 異遠 | 距離 |
|---|---|---|---|---|---|---|---|---|
| 1_Z | 1_G | 0.040459 | 1_L_N_F | 0.073554 | 2_Z | 0.093832 | 2_Z_N | 0.147471 |
| 1_L | 1_G | 0.061546 | 1_L_N_F | 0.127350 | 2_L_N_F | 0.147445 | 2_S_N | 0.205619 |
| 1_S | 1_S_N | 0.040530 | 1_L_N_F | 0.087137 | 2_Z | 0.117124 | 2_Z_N | 0.154932 |
| 1_G | 1_Z | 0.040459 | 1_L_N_F | 0.076769 | 2_L_N_F | 0.113339 | 2_S_N | 0.162701 |
| 1_T | 1_S_N | 0.040517 | 1_L_N_F | 0.082179 | 2_L_N_F | 0.108951 | 2_S_N | 0.149426 |
| 1_Z_N | 1_L_N_F | 0.039301 | 1_L | 0.120975 | 2_L_N_F | 0.104690 | 2_G | 0.133560 |
| 1_Z_N_F | 1_S_N_F | 0.012304 | 1_T | 0.075236 | 2_L_N_F | 0.090822 | 2_S_N | 0.138992 |
| 1_L_N | 1_Z_N | 0.040767 | 1_L | 0.076808 | 2_L_N_F | 0.099750 | 2_S_N | 0.137112 |
| 1_L_N_F | 1_Z_N | 0.039301 | 1_L | 0.127350 | 2_L_N_F | 0.085573 | 2_G | 0.130248 |
| 1_S_N | 1_T | 0.040517 | 1_L_N_F | 0.082951 | 2_L_N_F | 0.107986 | 2_Z_N | 0.139624 |
| 1_S_N_F | 1_Z_N_F | 0.012304 | 1_L | 0.106519 | 2_L_N_F | 0.090736 | 2_S_N | 0.140697 |
| 2_Z | 2_L | 0.070685 | 2_Z_N_F | 0.138728 | 1_Z | 0.093832 | 1_L | 0.160961 |
| 2_L | 2_L_N | 0.042585 | 2_Z_N_F | 0.119359 | 1_L_N | 0.104328 | 1_L | 0.148089 |
| 2_S | 2_G | 0.047779 | 2_Z_N_F | 0.095654 | 1_S_N_F | 0.109486 | 1_L | 0.169026 |
| 2_G | 2_S | 0.047779 | 2_Z_N_F | 0.097539 | 1_Z | 0.119786 | 1_L | 0.173317 |
| 2_T | 2_S_N | 0.052017 | 2_Z_N_F | 0.089151 | 1_L_N_F | 0.113199 | 1_L | 0.187217 |
| 2_Z_N | 2_S_N | 0.042733 | 2_Z | 0.091317 | 1_L_N_F | 0.094870 | 1_L | 0.201256 |
| 2_Z_N_F | 2_S_N_F | 0.025912 | 2_Z | 0.138728 | 1_Z_N_F | 0.099965 | 1_L | 0.155355 |
| 2_L_N | 2_L | 0.042585 | 2_Z_N_F | 0.108983 | 1_L_N_F | 0.107887 | 1_L | 0.190661 |
| 2_L_N_F | 2_L_N | 0.046180 | 2_Z | 0.076445 | 1_L_N_F | 0.085573 | 1_L | 0.147445 |
| 2_S_N | 2_Z_N | 0.042733 | 2_Z_N_F | 0.100042 | 1_L_N_F | 0.123904 | 1_L | 0.205619 |
| 2_S_N_F | 2_Z_N_F | 0.025912 | 2_Z | 0.122087 | 1_Z_N_F | 0.105750 | 1_L | 0.167878 |
分析
正しい順序(つまり、同一被写体と異なる被写体が的確に区別できている)となる率が向上しています。
前回の比較では、正しい順序となったケースは被写体1で6件、被写体2で2件、全体で8件でした。
今回の比較では、正しい順序となったケースは被写体1で8件、被写体2で6件、全体で14件と、精度的に向上していることが期待できます。
前回と同様に以下の観点でも整理してみましょう。
| 被写体1に関する最大距離 | 0.1273504217383994 |
| 被写体2に関する最大距離 | 0.13872850276387705 |
| 異なる被写体間の最小距離 | 0.08557307780107659 |
確実に同じ被写体と判別できる閾値は「0.08」であり、同じ被写体を撮影した場合でもそれ以上の距離となる場合は相変わらずあるようです。
閾値ごとの、成功例(同じ被写体と正しく認識できた)と失敗例(違う被写体を混同した)の推移に関しても見てみましょう。
| 指定された画像 | 0.08 | 0.09 | 0.10 |
|---|---|---|---|
| 1_Z.jpg | 10 / 0 | 10 / 0 | 10 / 0 |
| 1_L.jpg | 6 / 0 | 6 / 0 | 6 / 0 |
| 1_S.jpg | 9 / 0 | 10 / 0 | 10 / 0 |
| 1_G.jpg | 10 / 0 | 10 / 0 | 10 / 0 |
| 1_T.jpg | 9 / 0 | 10 / 0 | 10 / 0 |
| 1_Z_N.jpg | 9 / 0 | 9 / 0 | 9 / 0 |
| 1_Z_N_F.jpg | 9 / 0 | 9 / 0 | 9 / 2 |
| 1_L_N.jpg | 10 / 0 | 10 / 0 | 10 / 0 |
| 1_L_N_F.jpg | 6 / 0 | 9 / 1 | 9 / 3 |
| 1_S_N.jpg | 9 / 0 | 10 / 0 | 10 / 0 |
| 1_S_N_F.jpg | 9 / 0 | 9 / 0 | 9 / 1 |
| 2_Z.jpg | 3 / 0 | 7 / 0 | 8 / 2 |
| 2_L.jpg | 6 / 0 | 8 / 0 | 8 / 0 |
| 2_S.jpg | 9 / 0 | 9 / 0 | 10 / 0 |
| 2_G.jpt | 6 / 0 | 9 / 0 | 10 / 0 |
| 2_T.jpg | 8 / 0 | 10 / 0 | 10 / 0 |
| 2_Z_N.jpg | 7 / 0 | 9 / 0 | 10 / 1 |
| 2_Z_N_F.jpg | 3 / 0 | 4 / 0 | 6 / 1 |
| 2_L_N.jpg | 7 / 0 | 8 / 0 | 9 / 0 |
| 2_L_N_F.jpg | 10 / 0 | 10 / 0 | 10 / 0 |
| 2_S_N.jpg | 6 / 0 | 9 / 0 | 9 / 0 |
| 2_S_N_F.jpg | 5 / 0 | 7 / 0 | 8 / 0 |
| 被写体1 | 96 / 0 87% / 0% | 102 / 1 93% / 1% | 102 / 6 93% / 5% |
| 被写体2 | 70 / 0 64% / 0% | 90 / 0 82% / 0% | 98 / 4 89% / 3% |
| 全体 | 166 / 0 75% / 0% | 192 / 1 87% / 0% | 200 / 10 91% / 4% |
確実に異なる被写体を排除できる閾値「0.08」でも全体で75%の正解率です。
これは前回の分析において最適と判断した閾値「0.12」時の結果(正解率76%、誤認率3%)に匹敵します。
最もバランスが良いと思われる閾値「0.09」では全体の正解率が87%に向上し、誤認率もほぼ0%(1/242)です。
加えて被写体1と2の正解率の差も大きくありません(93%と82%)。前回の閾値「0.12」の結果では96%と56%で、40%の違いがありました。
閾値「0.10」では、正解率も若干向上しますが、誤認率も急増するので、前述したように「0.09」辺りを閾値とするのが最適であるように思われます。
まとめ
実のところ、今回の実験は半信半疑でした。
グレースケール化すると言うことは、色(正確には色相や彩度)に関する情報を放棄していることになるので、つまりは判別に使用できる情報(判断材料)が減っている訳ですから、精度的にはマイナスに働くのではないかと。
無論、当初の目的の一つが「撮影条件による色合いの変化の影響を軽減すること」だったので、色の重要度を下げたいとは思いましたが、丸っと放棄するのは少々極端ではないかと感じました。
しかし、結果としてはヒストグラム平坦化を行うことで、かなりの精度向上が期待できるとの感触を得ました。
現時点では実験対象が極めて限定的であるため、かなり過学習的な結論ですが、少なくともベクトル検索の精度向上に関する有効な手段の一つとしてキープしておく価値はありそうです。
同じラベル(エチケット)デザインで色違いのようなケースもあるかと思いますので、そのような場合にグレースケール化がどの程度マイナスになるのかが気になるところですが、その辺は今後の課題と言うことで。
